Culture: Population:
John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam The BWWJohn Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam The BWW SJohn Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam John Pellam The BWW Society The Bibliotheque World Wide Society The Institute for Positive Global Solutions Pellam Journal of Science Journal of Global Issues and Solutions
Data and Previsions On World Population
by Dr. Manuel Alfonseca
Escuela Politécnica Superior, Universidad Autónoma de Madrid, Francisco Tomás y Valiente, 11. 28049, Madrid, Spain, e-mail: manuel.alfonseca@uam.es
Historical previsions
The first scientist who analyzed the evolution of human population was Edmond Halley (1656-1742), who used the data collected by Caspar Neumann in Breslau (Wroclaw) about the number of births and deaths in his city and the age of people at death. Halley analyzed the data and built a life table showing the population in the city as a function of age. Noticing that the population was constant in those years, he used the following recursive formula:
P0(t+1) = B(t+1)
Pk+1(t+1) = Pk(t)- Dk(t)
where Pk(t) is the population aged k years at year t; B(t) is the number of births at year t; and Dk(t) is the number of deaths of people aged k at year t.
A few decades later, Leonhard Euler (1707-1783) generalized Halley’s equation for a population with constant growth, birth and death rates, as follows:
![]()
x=1+r
![]() .
.
where Pn is the population at year n, x is the constant growth rate, and Bn and Dn are the number of births and deaths at year n. In his computations he assumed a maximum human age of 100 years.
Since the end of the eighteenth century, apocalyptic warnings as regards the unstoppable increase of the world population have followed one another. In 1798, Thomas Robert Malthus published An essay on the principle of population, as it affects the future improvement of society, with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers. This essay includes the famous quotation:
Assuming then my postulata as granted, I say, that the power of population is indefinitely greater than the power in the earth to produce subsistence for man.
Population, when unchecked, increases in a geometrical ratio. Subsistence increases only in an arithmetical ratio. A slight acquaintance with numbers will skew the immensity of the first power in comparison of the second.
In 1838, as a reaction against Malthus and his alarmism, Pierre François Vermouth asserted in his Note on the law of population growth that this growth is not a geometric progression, but follows a logistic curve (see figure 1), which appears frequently in many natural growth processes and is the solution of the following equation:
![]()
The curve presents an inflection point at P=K/2, where K is an arbitrary parameter.
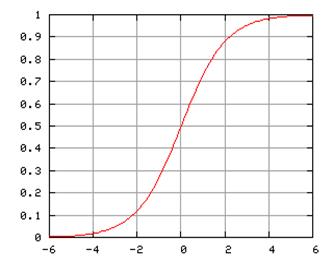
Figure 1. The logistic curve for K=1.
Verhulst tested his equation with a good fit against real data from France, Belgium and the U.S.A., but his predictions for the future 50 years did not come true, because his two parameters (the growth rate r and the limiting value K) are not really constant, but time dependent. With technology that increased the resources of the world along time, the value of K was increased above the value this parameter had around the mid-nineteenth century.
In spite of this, the first report of the Club of Rome (The limits of growth, 1972) insisted on an alarmist position by keeping to the previsions of Malthus (an exponential growth) without taking into account Verhoult’s study. In this context, several political and social movements have presented contraceptives and abortion as inevitable measures to save humanity from the disaster of overpopulation. A second, slightly less pessimistic report of the Club of Rome was published in 1974 (Mankind at the turning point).
In 2012 the UN published data about the growth of the world population from 1950-2010, which showed that the growth rate has declined, and that the turning point of the growth curve (which looks similar to the logistic curve) was crossed around 1985.
Based on these data, the UN have made three estimates of the future growth of the world population, one optimistic, one intermediate and one pessimistic. The first one (the low fertility scenario) predicted that a maximum of some 8300 million people will be reached by 2050. With the second one (the medium fertility scenario) the high point would be reached around 50 years later with nearly 11000 million people. In the worse prediction (the high fertility scenario) the maximum would be reached around 2150 in a much higher figure of total population, but the UN predictions do not reach farther than the year 2100.
Figure 2 shows the evolution of birth and death rates, according to the data and previsions of the UN, for the world and Europe. The three predicted scenarios can be seen in the figure. The maximum in the world population curve would be reached when the death rate became greater than the birth rate. It is easy to see that in the low fertility scenario this would happen around 2050. The high fertility scenario, on the other hand, looks unrealistic, as it assumes that the birth rate (which has been going down since 1950, from 37 to around 20) will in fact start growing again and then stabilize. Observe anyway that the death and birth rates have already intersected in Europe, which means that, without immigration, the population of Europe would be growing less by now.
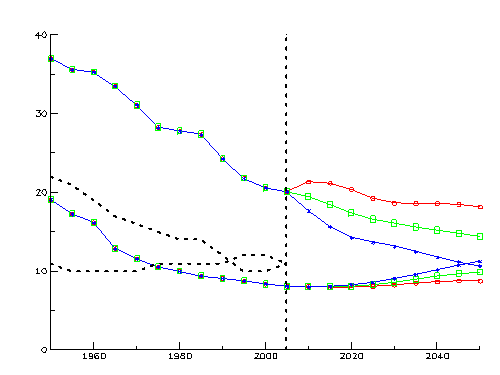
Figure 2. Birth and death rates along time for the world and Europe.
Based on these data, Julio Gonzalo and I have approximated the real growth of the world population and its extrapolation until 2050 by the following mathematical expression:
![]() ]
]
Figure 3 compares the U.N. data (real and predicted, in red) with those generated by the previous equation (in blue).
Result of the equation UN real & predicted data![]()
![]()
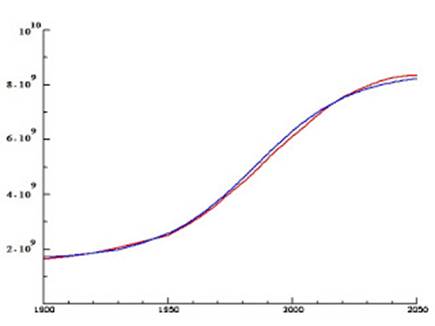
Figure 3. Birth and death rates along time for the world and Europe.
This equation depends on two parameters, α=0.5 ln(BR/DR) and t=500/Ö(BR.DR), whose evolution with time is shown in figures 4 and 5 for the three UN scenarios.
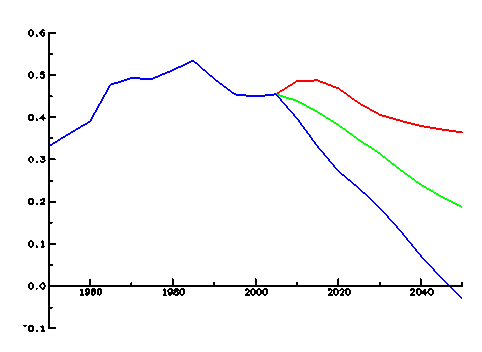
Figure 4. Evolution with time of parameter α.
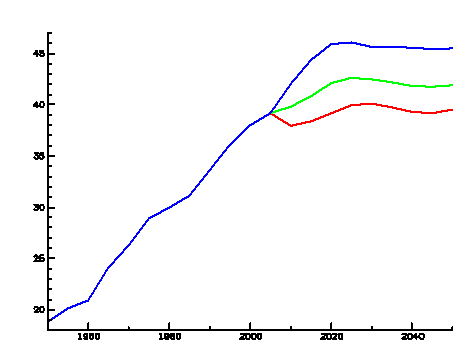
Figure 5. Evolution with time of parameter t.
It can be seen that the red curves (which correspond to the high fertility scenario) appear somewhat unrealistic, assuming that the value of α and t must remain constant in the future in the values they have just now, while the evolution of the low and medium fertility scenarios seems more reasonable.
In 2015 the UN published new updated data and formulated an even worse case scenario, where the African population would get completely out of control during the 21st century (see figure 6). This new scenario is even more unrealistic, as it assumes that the current birth rates in Asia and Africa will remain constant during the remainder of the century. If we take into account that the birth rate in Africa (still high) and Asia (where it is getting near the replacement level) have been decreasing steadily since 1950, this new scenario looks like an alarmist proposition.
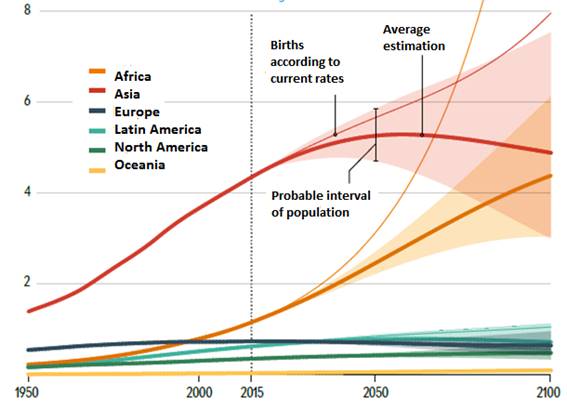
Figure 6. New UN predictions, updated in 2015.
Why this alarmism in the UN predictions? Because they want to promote the spread of abortionist politics in Africa, where most countries are opposed to those politics. However, using our above stated equation with the low fertility scenario, we have estimated the development of the world population if anti-natalist policies had not been implemented around the seventies. We have obtained the following results: the turning point would have been delayed until 1990, just five years later. By 2075 the population would have topped at 9 billion: 700 million more people, twenty five years later.
The inevitable conclusion is that anti-natalist policies do not give the expected results. This is now so obvious in China, that it has led them to put an end to their one-child policy. The hundreds of millions children sacrificed on the altar to Moloch have not been killed to save humanity, but so that we can share a little more for a little longer. It won’t be surprising if posterity accuses us of barbarism for allowing abortion against all scientific evidence, just as we accuse our ancestors for allowing slavery.